The study of how a ligand material, such as a hormone or antibody, binds to one or more kinds of molecular complexes, called sites, is of fundamental importance in biochemistry. Sites are often embedded in cell membranes, and the binding serves to control the behavior of the cell itself. Typically we are interested in the number of distinct kinds of sites and their frequency of occurrence, and also the equilibrium constants for each ligand-site binding reaction which indicates the absolute strength of each such binding reaction.
For example, quantitative analysis of hormone-receptor binding can be easily performed using appropriate software such as MLAB. MLAB is a computer program whose name is an acronym for "modeling laboratory"; it is an interactive system for mathematical modeling, originally developed at the National Institutes of Health. MLAB can fit multiple non-linear models to data points obtained from standard direct-binding or competitive displacement assays. Typical assays involve measuring the competition between radiolabelled and cold ligand in detergent-solubilized membrane preparations or on whole cells. Affinity constants and limit values of binding protein concentrations for single or multiple sites can be computed by fitting saturation curves in MLAB. Output can include Scatchard plots obtained by a suitable transformation.
There are two common categories of data. The first category results from cold displacement of bound labeled ligand where the labelled ligand concentration is held constant, the unlabelled ligand concentration is varied, and the ligand binding is calculated as a function of the proportion of labelled to total ligand concentration. The second category is a straight saturation analysis where the ligand binding is measured as a function of increasing labelled ligand concentration. This latter category of data also arises in fluorescent, ultraviolet, or electrical current studies. In general, MLAB can handle any measurements modeled by linear or nonlinear saturation plots.
In practice, the basic data must be adjusted to account for an experimentally-determined nonspecific binding level, specific activity of the labelled ligand, the values for maximal binding of the cellular preparations, and defective non-binding ligand. Replicate data points need not be averaged; they are entered as individual data points which are each included in the curve fitting process. In contrast, curve fitting based on dose averages may require careful attention to weights to obtain a reasonable fit. Experimental researchers rarely have a priori knowledge of the validity of individual data points, so each point is generally assigned an unbiased equal weight. However, weighting functions can be differentially applied in MLAB to adjust for differing error percentages, such as may occur in measurements of low levels of radioactivity. Because of the options for flexible weights, MLAB addresses some of the problems inherent in the treatment of experimental data where the number of samples is usually low and the error can be relatively high.
MLAB can be used to analyze down and up regulation in receptor number on the cell surface, where the binding capacity or receptor concentration is the limiting -intercept on the Scatchard plot. The MLAB program is also useful in determining whether changes in binding by different ligand agonists/antagonists can be attributed to reduced binding affinity of the defined site/sites (seen as changes in the affinity constant), or to the total loss of binding ability of a class of sites (seen as changes in the binding capacity, and changes in the fit from an to site model). Similarly, MLAB can aid in comparison studies of a single ligand against different binding proteins that vary by site-directed mutagenesis, or alternative splicing; such analyses can be useful in exploring mechanisms of ligand/receptor interaction, including amino acid and charge requirements.
In addition, post-translational processing and folding of the nascent protein in the endoplasmic reticulum can be studied by estimating the number of active receptor molecules that have reached the cell surface. These studies are of current interest to biochemists, and an accurate method of quantification is important since conclusions about the biological system, which in turn determine the future direction of research, are based on the calculated binding parameters.
In addition to saturation and Scatchard analyses, MLAB can be used in many other curve fitting applications such as kinetic, Michaelis-Menten, Lineweaver-Burke plots, and various statistical analyses. Kinetic analysis involves fitting differential equation models, which is an important core capability of MLAB.
MLAB has hundreds of useful functions, e.g., the discrete Fourier transform function dft and the parametric spline interpolation function splinep. One of the central components of the system is a curve fitting program which will adjust the parameters of a model function to minimize the weighted sum of the errors raised to a specified power. A repertoire of mathematical operators and functions, routines for solving differential equations, a collection of routines for onscreen drawing and for hardcopy plotting, and mechanisms for saving data between sessions provide a powerful and convenient environment for data manipulation, arithmetic calculations, and for building and testing models.
The user communicates with MLAB by typing commands which are executed at once or by providing a script to be executed. Should the user have questions, typing HELP will put the on-line system documentation at his disposal. The MLAB language is defined in the MLAB reference manual.
One of MLAB's main uses is to fit models to data. Curve-fitting is a useful analytical tool in many diverse disciplines. The basic notion is easily described. Given data, say various points in the plane , , ..., , and a function where involves some parameters, say and , as for example , we may wish to calculate values for the parameters
The curve-fitting and graphics display facilities of MLAB make it an ideal tool for the estimation of equilibrium constants from data, which typically consist of observed amounts of ligand bound for various specified amounts of ligand provided for binding.
Suppose we have a ligand, , which binds to each of independently-acting sites, , , ..., , which are present in the various concentrations of mmol, mmol, ..., and mmol respectively. Each reaction forms a bound complex , and we shall define to be the associated equilibrium constant. Let denote the concentration of ligand present initially, and let be the concentration of free ligand at equilibrium. Similarly, let denote the concentration of free sites of type at equilibrium, and let denote the concentration of bound site complex at equilibrium. Note we use the symbols , , and for the numerical quantities in millimole units of these materials, as well as for the names of the materials themselves. Then: and for and
Note that is specified in liters/e units, so that is the corresponding equilibrium constant in liters/mole units.
Often there is a fictitious -st site, , which binds molecules, which is introduced to describe the non-specific binding of molecules with weak affinity to many locations, other than the specific sites of interest. Let be the equilibrium constant for the fictitious non-specific binding reaction F + X <--> Y. Then we have:
where is the concentration of non-specifically bound ligand, is the concentration of the fictitious non-specific binding site, and is the concentration of the free fictitious site at equilibrium. Then for , and .
Now, to capture the notion of non-specific binding as a weak sticking of molecules almost everywhere, let tend to zero and let tend to infinity such that , where is a fixed constant. Then , and we have: for and
Note that the mathematical form is difficult to handle when approaches 0, or when approaches 0, so that the form given above is more convenient.
Usually values of and/or are measured for different values of and we wish to use this data, which is generally of the form or , to estimate , , ..., , , and, if not already known, , , ..., . When only the total bound concentration is measured, rather than , , ...,
Often people use the model and fit it to data points of the form where is the free ligand concentration at equilibrium and is the total bound ligand concentration at equilibrium, with one such point for each experiment. The difficulty with this approach is that we must compute as so that there is correlated error in both the dependent and independent values used to form the data points. Our approach uses data points of the form , and since can usually be accurately determined, our model avoids the aforementioned difficulty of error in the independent variable.
It is possible to model the simultaneous use of several distinct types of ligands having distinct binding-affinities interacting with multiple classes of sites. This can be done by a straightforward elaboration of the equations used above. Although we shall not provide an example here, this is an important situation to be kept in mind.
The general two-site model with non-specific binding for a single ligand type can be defined in MLAB with the following dialog. Here and hereafter, the text shown following the MLAB prompt asterisk is an MLAB command statement entered by the user.
* FUNCTION B(F) = k1*S10*F/(1+k1*F) + k2*S20*F/(1+k2*F) * FUNCTION F(F0) = ROOT(Z,0,F0,F0-B(Z)-Z*(1+c)) * FUNCTION Y(F0) = c*F(F0)Here for .
These commands exemplify the MLAB FUNCTION statement, which is used to define a function or differential equation. Note that arguments of functions must be explicitly specified. Variables, such as k1 and k2, which appear in the body of a function, but not in its argument list, are called parameters. Parameters must be assigned values before an associated function can be evaluated.
ROOT is an operator which is built-in in MLAB. ROOT(Z,A,B,E) is a value between A and B which, when taken as the value of the dummy variable, Z, makes the expression, E, which involves Z, equal to zero. Thus ROOT(Z,A,B,E) is a solution of . The model given above, involving a so-called implicit function, deserves careful study; it is easily extendible to more than two sites. The amount of free-ligand at equilibrium as a function of satisfies .
Suppose we have measured in mmol units as a function of in millimole units, as follows:
F0 F
.58668 .036
1.1734 .096
2.3467 .385
2.9334 .61
4.1068 1.15
4.6934 1.46
5.8668 2.11
7.0402 2.73
and suppose we have mmol. (If and
were unknown, we could include them as fitting parameters.)
Then, we can introduce the appropriate constraints (which should always be used for this particular model), guess , , and and then estimate them, as follows.
* constraints q ={k1>=0,k2>=0,c>=0,S10>=0,S20>=0}
The CONSTRAINTS statement permits the user to specify successive linear inequalities or equations involving the parameters (or potential parameters). Now we may specify values for the parameters, guessing when necessary.
* k1 = 10; k2 = 1; c = 0; S10 = 1.7121; S20 = S10;
Here the ASSIGNMENT statement is exemplified. In this case all the above assignments are assigning values to scalar variables, but the assignment statement is used to assign values to matrices as well. This can be seen in the next assignment statement which defines a matrix, .
* D = Kread(8,2) .58668 .036 1.1734 .096 2.3467 .385 2.9334 .61 4.1068 1.15 4.6934 1.46 5.8668 2.11 7.0402 2.73
The KREAD operator takes optional array size arguments; in this case an 8 row by 2 column matrix is specified, and reads in numbers from the keyboard to construct an appropriately-dimensioned matrix as the result. An analogous function is used to read numbers from a file. This matrix is then, in this case, assigned to D. Note the entry of the numbers which follow. Now we may examine D by "typing it out" using the TYPE statement.
* type D D: 8 by 2 matrix 1: .58668 .36E1 2: 1.1734 .96E-1 3: 2.3467 .385 4: 2.9334 .61 5: 4.1068 1.15 6: 4.6934 1.46 7: 5.8668 2.11 8: 7.0402 2.73
We have established a model function, , and entered data, . Expect for error, we expect that would hold, if only the parameters , , and were set to their "correct" values. The following FIT statement requests MLAB to estimate , , and by assigning them values which minimize the sum-of-squares objective function .
* maxiter = 30; TOLSOS = .001 * fit(k1,k2,c), F to d, constraints q final parameter values value error dependency parameter 13.86352736 2.331373145 0.665073064 K1 0.5321372226 0.06602915638 0.9432600296 K2 0.5874015019 0.02229743988 0.9171690302 C 5 iterations CONVERGED best sum of squares = 9.78763e-04 root mean square error = 1.39912e-02 deviation fraction = 6.82654e-03 R squared = 9.99854e-01 no active constraints
The behavior of the fit statement depends upon the supplied constraints , as well as upon the MLAB control variables: maxiter, the maximum number of iterations and tolsos, the requested convergence factor.
MLAB uses a carefully-tuned version of the Marquardt-Levenberg magnified-diagonal algorithm which is, in turn, a form of the Gauss-Newton procedure for minimizing a function which is in the form of a sum-of-squares. This process estimates the value of the parameter vector by successive approximations , , ..., , where is the vector of initial guesses for , , and , and , where
where is the estimated covariance matrix of the observations. In our example, , the identity matrix. In general is determined from weight-values supplied by the experimenter.
An iteration consists of computing from . Note that this requires the partial derivatives of the model function with respect to the parameters evaluated at , since these values form the matrix . In MLAB, these derivatives are automatically computed symbolically and evaluated to form . The convenience thus obtained is considerable and the parameter estimation process is provided with more accurate derivative values. For example the derivative of with respect to can be explicitly displayed in MLAB as follows.
* type F'k1
FUNCTION F'K1(F0) = EVAL(Z,ROOT(Z,0,F0,(F0-B(Z))-Z*(1+c)),
-B'K1(Z)/(B'F(Z)-(1+c)))
Indeed derivatives are full-fledged members of the class of functions and can be used in graphics or curve-fitting in MLAB just as can any other user-defined function.
A sub-iteration consists of computing with a particular value of which specifies the amount of diagonal magnification. At each iteration, the value starts at and is increased until the corresponding value of results in a smaller sum-of-squares value, whereupon this vector is taken to be the final iterate.
The parameter estimation process stops when the limit of the number of iterations is reached or, more usually, when the decrease in the sum-of-squares value between successive iterations is less than a specified fractional amount determined by the user-specified convergence factor in TOLSOS. For TOLSOS, the sum-of-squares must change by less than percent for the curve-fitting process to stop based on this criterion.
When the estimation process does stop, the parameters are reset to their computed estimates, and they and their estimated standard deviations are typed-out. Associated values called dependency values, which lie between 0 and 1, are also typed-out. It suffices here to remark that large dependency values above usually indicate a non-unique solution; that is, other parameter estimates exist which would provide a nearly equally-small sum-of-squares.
MLAB also types-out the root-mean-square error which is the estimate of the standard deviation in each observation, given that they are identically distributed. This quantity should roughly equal the experimental error in the data. There are, of course, many caveats and restrictions which must hold to insure the validity of the supporting statistics provided.
The material typed out above shows that the vector of parameters has been estimated to be , with reasonably small dependency values and standard error values, and with an RMS error of about , which should be comparable with the experimental error in our data, . The sum-of-squares was reduced from an initial value of to at the final parameter values.
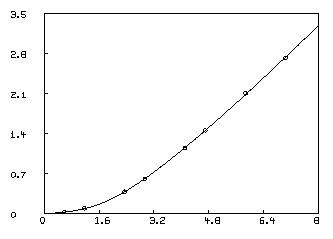
In order to visually see how our model with its parameters set to their best-estimated values corresponds to the data, we may draw a graph of the data points and the model function. Although we are drawing only the simplest and most direct kind of picture here, it should be noted that MLAB provides facilities for many types of point-symbols and types of lines, axes with arbitrarily-placed numeric labels in various formats, titles in the form of text strings in arbitrary sizes and various fonts with subscripts and superscripts, color, and a number of other special features. It is quite possible to prepare more or less elaborate publication-quality graphs with a modest amount of effort. Indeed this is one of MLAB's most-used facilities. The desired graph can be constructed as follows.
* draw D, linetype none,pointtype circle * draw c2 = points(F,0:8:.2) * VIEW
The first DRAW command above plots the data points, while the second draw command constructs a curve called C2, which is a graph consisting of solid straight-lines connecting the points which are the rows of the 2-column matrix which is the value of the expression POINTS(F,0:8:.2). This matrix has the values 0 through 8 in steps of in its first column and corresponding values of the function evaluated at 0 through 8 in steps of in the second column. The POINTS operator is very useful for graphing functions. Both these curves are drawn in the default MLAB 2D-window called W (since no other window is specified) which has predefined labeled axes already present. The picture finally appears when its display is requested with a view statement and a plot can be obtained if desired using the PLOT statement.
Often a Scatchard graph of Bound/Free vs. Bound (i.e., vs. ) is desired. Although such a formulation should not be used for curve-fitting due to the non-normal error introduced by computing Bound/Free, it is quite straightforward to draw the data and model Scatchard plots as follows. Note the current picture in W is saved and restored.
* SAVE W IN GW * DELETE W * FUNCTION R(X,Y)=IF Y=0 THEN (k1*s10+k2*s20) ELSE X/Y * MF = F ON 0:8:.2 * M = B ON MF * M = M&'(R ON M&'MF) * DRAW M; * MF = D COL 2 * M = (D COL 1)-(1+C)*MF * M = M&'(R ON M&'MF) * DRAW M, LINETYPE NONE, POINTTYPE "o" * TOP TITLE "Bound/Free vs. Bound" * VIEW
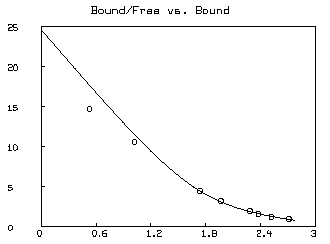
* DELETE W,MF,M * USE GW
The &' operator denotes column concatenation, while the ON operator, as in F ON H, applies the function F to each row of the matrix H treated as an argument list for F and returns the column vector of result values.
It is an enlightening exercise to fit the Scatchard model to the corresponding transformed data and to then draw a graph of the original data points and the function using the parameter values obtained. An example of this comparison is given in the following section.
If we know we have non-cooperative two-site specific binding, with our given and values, together with non-specific binding with no degradation (degradation could be due to the presence of various enzymes for example), then this curve-fit of the correct model gives us the best available estimates of , , and . But if the model is possibly not correct, we have a more difficult problem of deciding what the correct model is. This often cannot be resolved without further experimentation.
The non-specific binding constant, , can be independently estimated by adding a large amount of unlabeled ligand, , which is distinguishable from , to a mixture of and the site-bearing material. Then virtually all the bound which results will be non-specifically bound and taking this value as yields the approximation . With a value of known from one or more such experiments,
If we have no such independent estimate of , and we are unsure if non-specific binding is occurring, we may test the unrealistic possibility that there is no non-specific binding as follows.
* tolsos = .0002 * c = 0 * fit(k1,k2), F to d, constraints q final parameter values value error dependency parameter 10.42883512 881.9654883 0.9989885554 K1 10.87461407 712.3997932 0.9989885554 K2 27 iterations CONVERGED best sum of squares = 1.31885e+00 root mean square error = 4.68838e-01 deviation fraction = 2.57765e-01 R squared = 8.02989e-01 no active constraintsLSQRPT is a sum of zero or more of the values 1, 2, 4, and 8. When LSQRPT contains 1, the best sum of squares obtained at each iteration is typed-out. When LSQRPT, the fit command directs MLAB to type-out only the final results. All intermediate reports are suppressed. It is also possible to use LSQRPT which suppresses all output, but the parameters are reset as usual. In any event, a matrix called COVP (the estimated covariance matrix of the parameters) and a scalar called SOSQ (the final sum-of-squares value) are created, replacing any previous data objects with these names. The user may examine these values, or employ them in further calculations as desired.
We may examine our fit by redefining the curve C2.
* draw c2 = points(F,0:8:.2); view
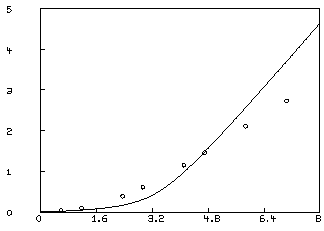
This is not an adequate fit, as we could have predicted by noting the large parameter standard deviations and the large RMS error. Although the dependency values are not extremely close to one, we may consider the possibility that our fit is bad because we fell into an unfortunate local minimum. A crude way to study this possibility is to draw a contour map of the sum-of-squares surface to see if several local minima are apparent. This is possible in this case, since we have fewer than three parameters, and MLAB can be used to view the sum-of-squares surface as follows. Drawing this contour map is time-consuming due to the large number of root calculations required.
* FUNCTION FH(F0,K1,K2)=ROOT(Z,0,F0,F0-(K1*S10*Z/(1+K1*Z)
+K2*S20*Z/(1+K2*Z))-Z*(1+C))
* FUNCTION S(k1,k2)=SUM(I,1,8,(FH(D[I,1],k1,k2)-D[I,2])2)
* M=contour(points(S,cross(0:20,0:20)),1.3:1.35:.005&1.4:1.8:.2&2:5)
* DELETE W
* DRAW M, LINETYPE VMARKER; VIEW
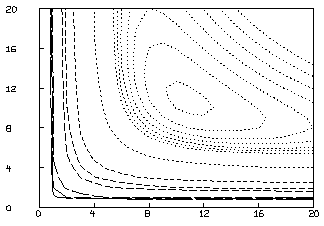
The CROSS operator expression above constructs a 441 by 2 matrix whose rows are all the pairs with . The CONTOUR operator expression constructs a specially-coded two-column matrix which is suitable for drawing with line-type VMARKER. Contour lines are formed for the surface height values in the list 1.3:1.35:.005 & 1.4:1.8:.2 & 2:5 where & denotes row concatenation. Evidently, our solution is unique.
We may try a one-site model with equal to by using our two-site model where both sites are identical as follows. If were not known, we could add S10 to the parameter list to be adjusted.
* S10 = S10+S20; k2 = 0; * fit(k1,c), F to d, CONSTRAINTS Q final parameter values value error dependency parameter 2.325176617 0.2567377717 0.5948957102 K1 0.4642651058 0.03442515131 0.5948957102 C 15 iterations CONVERGED best sum of squares = 1.55348e-02 root mean square error = 5.08835e-02 deviation fraction = 2.31134e-02 R squared = 9.97679e-01 no active constraints *delete w *draw D, line none, pointtype circle *draw points(f,0:8:.2); VIEW
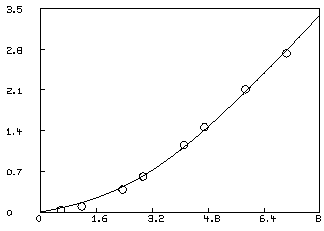
This fit is not as good as the fit obtained with the two-site model, and we can probably reject it. We should have an estimate of the variance of the data in order to test the goodness-of-fit. Even with curve-fitting evidence, it is best if there is independent evidence of multiple sites. Also, of course, a three or more site model, with or without non-specific binding may be the correct model.
Thus, in general, given the correct model, curve-fitting is a powerful device for estimating parameters; but curve-fitting is not always a very good way to distinguish the correct model from alternate impostor models. Usually we must resort to discriminating experiments.
MLAB can handle simultaneous curve-fitting, where several functions are to be fit to corresponding sets of data points and where, moreover, these several functions share some parameters in common. MLAB model functions can be functions of more than one formal argument, so that data points may lie in -space for arbitrary , but we do not provide an example here. However we shall provide an example of simultaneous curve-fitting.
Suppose we not only have the data given above for 2-site binding, but also are given the following observations of the concentrations of -ligand which is non-specifically bound, for various amounts of ligand provided initially, denoted by .
F0 Y 1.1734 .3 2.5 .5 3 .3 3.98 .7 6.5 1.6
Then we may enter this data as the rows of a matrix and estimate k1, k2, and c based on all the available data.
* N=KREAD(5,2) 1.1734 .3 2.5 .5 3 .3 3.98 .7 6.5 1.6
In general, we should use weights which specify the relative accuracy of each data point. For each data matrix, a vector of weight values may be given as a clause in the FIT statement. The weight-value, , that corresponds to an observation should be . Of course, guesses or estimates must generally suffice. The value for corresponds approximately to a constant percentage error in the observed value . Weight functions are permitted in MLAB, and a more accurate device is to use the reciprocal of the square of the model function itself as the weighting function; this results in an iterative reweighting process.
The use of weights permits data points of high reliability to exert greater influence on the parameter estimates than data points of lesser reliability. When simultaneous fitting is being done, weights have the additional function of compensating for differing units or magnitudes of the observations from various data sets. Without weights, the curve-fitting process would tend to favor one model component, fitting it at the expense of others, if the deviations there were much larger than the others, even though this may be an artifact of the use of different units.
MLAB includes an operator, EWT, which computes a vector of weight-values for a given set of data points, M, by estimating the standard deviation at each point by the difference between the data curve and a smoothed form of it, which effectively assumes the error is due to white noise. These standard-deviation estimates are, in turn, smoothed, and then used to form reciprocal variance weight values. In our example, we shall use EWT to obtain the necessary weight vectors, although this is not totally appropriate for chemical binding data, which is often taken in a range where the measurement accuracy improves as the amount of bound ligand increases. Also, EWT is unreliable for small numbers of data points. Nevertheless, we shall proceed as follows.
* DW = EWT(D); DN = EWT(N) * TYPE D&'DW,N&'DN : a 8 by 3 matrix 1: 0.58668 0.036 340.092919 2: 1.1734 0.096 340.092919 3: 2.3467 0.385 271.140209 4: 2.9334 0.61 256.511957 5: 4.1068 1.15 193.017413 6: 4.6934 1.46 171.441311 7: 5.8668 2.11 93.14747 8: 7.0402 2.73 93.14747 a 5 by 3 matrix 1: 1.1734 0.3 159.445918 2: 2.5 0.5 159.445918 3: 3 0.3 156.341715 4: 3.98 0.7 134.665471 5: 6.5 1.6 134.665471 * fit (k1,k2,c), F to d with weight dw, Y to n with weight dn, CONSTRAINTS q Begin iteration 1 bestsosq=5.86711e+01 Begin iteration 2 bestsosq=2.76531e+01 Begin iteration 3 bestsosq=2.69881e+01 final parameter values value error dependency parameter 1.681292363 0.3984166729 0.6190759098 K1 1.905413519e-17 0.06987097833 0.6367292361 K2 0.6401358429 0.057666687 0.09280130233 C 3 iterations CONVERGED best sum of squares = 2.69879e+01 root mean square error = 1.64280e+00 deviation fraction = 6.88260e-02 lagrange multiplier[1] = -0 lagrange multiplier[2] = -73.23991748 lagrange multiplier[3] = -0 * delete w * draw d line none pt circle * draw points(F,0:8:.2) * draw n line NONE pointtype "+" * draw points(Y,0:8:.2) linetype dashed * VIEW
As mentioned above MLAB also allows weights to be the reciprocals or other functions of the actual squared deviations themselves. This device is called curve-fitting with iterative reweighting and is invoked in MLAB by specifying an appropriate weight function. Moreover MLAB employs an iterative reweighting technique to allow the general form of a sum of pth powers to be minimized, rather than just a sum-of-squares. This so-called -norm fitting is sometimes useful for or when the data is not normally-distributed, and tends to contain some outliers. The value is specified as the value of the MLAB control variable fitnorm.
Given a radioactively-labeled ("hot") ligand material F, we wish to mix varying amounts of hot ligand each with the same fixed amount of site material, and obtain a table of the amounts of bound ligand corresponding to the total amounts of ligand added. This requires that we be able to separate the bound ligand from the free ligand and then measure the amount of bound ligand by the numbers of radioactive-decay events per minute for each distinct experiment.
There is an alternate device which sometimes has an advantage in simplicity over this direct method. Let us add a single fixed amount of hot ligand to the site material and then add varying amounts of unlabeled ("cold") ligand. The cold ligand form of F competes with the hot ligand in binding to the sites, and the effect is that as we add more cold ligand, the observed concentration of bound hot ligand decreases. We may sometimes be able to add an incremental amount of cold ligand to our mixture, separate and measure the amount of bound hot ligand, and then remix and add the next incremental amount of cold ligand; when this is possible, the variability due to differing concentrations of sites and hot ligand is reduced. Since replicate experiments suffer from using slightly-differing amounts of site material and of hot ligand, it is often better to expend effort getting more points for a single sample of site material than to run replicate experiments (except as a gross check on the experimental process.) In any event, the results of replicate experiments need not be averaged; the MLAB curve-fitting process will, in effect, give each point equal weight as is appropriate.
We have a further complication to deal with. Both the hot and cold ligand materials usually bind weakly and non-specifically throughout our mixture, in addition to specifically binding with the site material. The amount of such non-specifically bound hot ligand is generally taken to be proportional to the total amount of hot ligand present less the amount bound, i.e. for some constant where denotes the concentration of free hot ligand at equilibrium. Let denote the concentration of bound hot ligand, both specifically and non-specifically, and let denote the concentration of specifically-bound hot ligand. The concentration of hot ligand in all forms is . Then . If we add a very large amount of cold ligand to our mixture, almost all the specific binding sites will be occupied by cold ligand. The amount of observed bound hot ligand may then taken to be the amount of non-specifically bound hot ligand , whence is approximately equal to . We can thus use our other observed values and compute corresponding values by subtracting from the values, where has been estimated as indicated above. (Alternatively, it is possible, and generally preferable, to curve-fit for the unknown non-specific binding constant as is done below.)
In any event, for each observation point, we know the constant Molar concentration of hot ligand present, the concentration of cold ligand present and the observed concentration of bound hot ligand (with due regard for the volume of the mixture). Computing the concentration requires a computation based on the following parameters.
Then we have Molar units (M) of hot ligand. As a check, . This equation can alternately be used to determine any of the other parameters involved, given in Molar units. In particular, if the observed value of is not close to the predicted value from this equation, there is some difficulty in the experimental parameters. The corrected value of we use in subsequent calculations is then obtained by multiplying by the bindable fraction factor . The concentration in Molar units of the bound hot ligand is computed as .
The concentration of cold ligand is M. (If a fraction of cold ligand is inert, the corresponding correction should be made to .) A series of competition experiments consists of varying and observing the differing values of (and potentially ) that result. The final outcome is a sequence of (,,) triples, where and vary, and is generally fixed. For a series of direct-binding experiments, is 0, and we vary directly. The result is a sequence of (,,) triples where and and vary.
Let us consider a single-site material . Suppose our mixture contains a concentration of M of this site material together with M of cold ligand and M of hot ligand. Our goal is to estimate the equilibrium constant of the reaction . Let denote the concentration of bound cold ligand at equilibrium and let denote the concentration of free (unbound) cold ligand at equilibrium, just as and denote these quantities for hot ligand. Suppose the reactions and have the not-necessarily-equal equilibrium constants and , so that and , where denotes the concentration of free sites at equilibrium. Also, , , and . All concentrations are in Molar units (M).
Our goal is to estimate , given the varying observed concentrations of bound hot ligand associated with the sequence of cold ligand concentrations used. This cannot be done without knowing , or alternately, the ratio . Thus , and either or , but not both, is to be determined. Often we may assume .
A pre-computer-style Scatchard-plot analysis method is often employed to estimate the equilibrium constant . When , suppose that , where is known. Also we have and . Then , or . This last relationship is a linear relation between and . If we graph vs. for varying amounts of , we obtain a straight-line graph with slope and -axis intercept and -axis intercept . Note that is a dimensionless quantity, so we could compute and separately in any desired units (such as cpm), and obtain the same ratio when is formed. This is the so-called Scatchard plot commonly used when a more advanced analysis is not available; the unknown parameters and are estimated directly from looking at a straight-line fit of the experimental points (,). Then . As increases, both and increase, but increases faster; this is reflected in the fact that the Scatchard plot line has a negative slope. If the plotted points do not approximately lie on a negatively-sloped straight line, the one-site binding model that has been assumed is probably incorrect. (What do you think about the example presented below?)
For a sequence of competitive binding experiments, the crucial point is that when we have % hot ligand and % cold ligand, then both forms of ligand participate in every chemical state in this proportion (modified by the equilibrium proportionality constant .)
When , so that , we then have . And and , where . Thus , so , analogous to the non-competitive binding case!
In general, however, it is preferable to use the data (,), where and , and fit the model given above for multiple-site binding with a single ligand where the independent variable is the total concentration of (hot and cold) ligand supplied, and the dependent variable is the concentration of (hot and cold) ligand bound (specifically and non-specifically). When is not, using this model is required.
Thus we may construct the data points (,) where and for each experimental data point (,,), and then fit the function to this data in order to estimate the parameters , , , (and , , if a two-site model is desired). When is not, we introduce the constraints and and use the two-site model for the one-site situation with is not.
A general do-file based on the MLAB statements given above can be constructed which queries the user for the experimental parameters: , , , , , , , , , and for the sequence of value-pairs , and then fits the desired model, reports the estimated values of , , and , and graphs the corresponding saturation plot and Scatchard plot for the data. A simplified example of such a do-file (called liganal.do is shown below, together with an example of its use.
"liganal.do = competitive single site binding analysis"
echodo=0 /* echodo=0 inhibits screen and log-file output */
reset
namesw=0
type "Specify the COLD ligand molecular weight"
wc=kread("wc=")
type "Specify the HOT ligand molecular weight"
wh=kread("wh=")
type "Specify the half-life in days of the HOT ligand label"
hl=kread("hl=")
type "Specify the age in days of the HOT ligand label"
al=kread("al=")
type "Specify the counting-efficiency (c+/-/d+/-) of the label"
ce=kread("ce=")
type "Specify the counting time-period in minutes"
ct=kread("ct=")
type "Specify the background radioactivity in cpp(counts per period)"
br=kread("br=")
type "Specify the specific activity of the HOT ligand(in d+/-/mole)"
sa=kread("sa=")
type "Specify the total counts per period of HOT ligand(in cpp)"
tc=kread("tc=")
type "Specify the HOT ligand bindability fraction"
bd=kread("bd=")
type "Specify the Volume (in milliliters)"
v=kread("v=")
type "Specify the mass in ng of the HOT ligand
(or enter -1 to have the mass computed for you.)"
mh=kread("mh=")
/*Compute the mass in ng of the HOT ligand! */
mhx=(v*wh*1e6)*(1e3/sa)*(tc/(ct*ce))*(2(al/hl))/v
type "specified mh value (in ng):", mh
mh=mhx
type "computed mh (hot mass) value (in ng) based on tc:",mh
type "Specify the number of experimental observation points"
nb=kread("nb=")
type "type-in the sequence of "+strval(nb)+" data points"
type "as: ([COLD ligand mass in ng], [observed bound cpp]) pairs"
type "on successive lines"
namesw=1
d=kread(nb,2); d=sort(d)
/* 2 classes-of-sites binding model.
We use k2=0 and s20=0 for the 1-class-of-sites specialization*/
FCT A(F0)=G(F(F0))
FCT G(F)=B(F)+C*F
FCT B0(F0)=B(F(F0));
FCT B(F)=K1*S10*F/(1+K1*F)+K2*S20*F/(1+K2*F);
FCT F(F0)=ROOT(Z,0,F0,F0-B(Z)-Z*(1+C));
FCT Y(F0)=C*F(F0);
CONSTRAINTS CQ={K1>=0,K2>=0,C>=0,S10>=0,S20>=0};
lh=mh/(wh*v*1e6)
lhck=(tc/(ct*ce))*(1e3/sa)*(2^(al/hl))/v
namesw=0
type "Molar conc. of HOT ligand based on supplied molecular wt.",lh
type "Molar conc. of HOT ligand based on total cpp supplied",lhck
namesw=1
lh=lh*bd /* compensate for inert hot ligand */
fct m0(x)=if x>0 then x else 0
fct cconc(mc)=mc/(wc*v*1e6)
fct bconc(a0)=((a0-br)/(ct*ce))*(1e3/sa)*(2^(al/hl))/v
dm col 1 = cconc on (d col 1) /*total cold (M)*/
dm col 2= m0 on bconc on (d col 2) /*bound + non-spec. bound (M)*/
/*type-out the raw and converted input data*/
type "D=input data [Cold Ligand (ng) | Hot counts]", d
type "DM=[Cold Ligand (M) | Hot Spec.+Non-Spec.bound(M)]",dm
/* compute da col 1= LH+LC, da col 2= AH/alpha */
da=lh+(dm col 1) /*total (hot+cold) */
alpha=lh/'da /* vector of scale-factors*/
da col 2=(dm col 2)/'alpha /* scaled bound+non-spec. bound */
/* compute guesses for K1 and S10 from the Scatchard fit.
estimate C from the largest cold ligand data point. */
i=maxrow(dm col 1);
c=m0(dm[i,2]/(lh-dm[i,2]))
fre=lh-(dm col 2) /*free hot (FH) in Molar units */
yns=c*fre /*non-spec. bound hot */
sd =m0 on ((Dm COL 2)-yns); /* spec. bound hot*/
sd2 = sd/'fre /*bound/free */
sd col 2=sd2
sd col 1 = (sd col 1)/'alpha /* spec. bound (all =H+C) */
sd=compress(sd);
type "directly-estimated non-spec. binding coef.", c
ltot=(da col 1)
ftot=((da col 1)-(da col 2))
ytot=yns/'alpha
btot = sd col 1
mmt=ltot&'btot&'ytot&'ftot
type "MMT=[L Total | B Total | Y Total | F Total]", mmt
mmh=mmt/'(alpha^^'4)
type "MMH=[L Hot | B Hot | Y Hot | F Hot]", mmh
mmcOA=mmt-mmh
type "MMC=[L Cold | B Cold | Y Cold | F Cold]", mmt
/*Remember BH/FH = -K1*BH/alpha +K1*S10 */
fct lin0(b)=-k1*b+k1s10 /* simple linear form */
fct lin(b) = -k1*(b-s10)
k1=1; k1s10=lh
lsqrpt=0
fit(k1,k1s10), lin0 to sd
s10=k1s10/k1
fit(k1,s10),lin to sd
type "Scatchard model linear-regession fit estimates",k1,s10
ok1=k1; os10=s10
draw sd lt none pt circle color orange
draw points(lin,0:s10!4) lt dashed
top title "Scatchard plot"
title "[dashed=regression-fit line]" at (.5,.75) fract size .14 inches
title "[hashed=euclidean-fit line]" at (.5,.7) fract size .14 inches
/* compute k1 and s10 for the best euclidean-fitting line */
qb=mean(sd)
q=sd-(qb')^^nrows(sd)
m=q'*q
z=eigen(m) row (1,3,5)
rno=if z[1,1]>z[1,2] then 2 else 3
v1=(z row rno)'
k1=-v1[2]/v1[1]
s10=(qb[2]-v1[2]*qb[1]/v1[1])/k1
type "Scatchard model euclidean-fit estimates;", k1,s10
draw points(lin,0:s10!50) pt nbar ptsize .01
unview;
ws=w; blank ws;
k2=0; s20=0;
/*define our weighting function (fixed-percentage error assumed) */
fct wvf(x)=1/x^p>
p=2;
wv1=.00000001*(wvf on (da col 2));
lsqrpt=8
maxiter=90
FIT(K1,s10,C),A TO da with wt (wv1), CONSTRAINTS CQ;
/* Draw the (full) relative saturation curve log-plot form ------------*/
FL = (da[1,1]*.9):((da[nrows(da),1])*1.1)!100;
am= POINTS(a,FL);
lda= (log on da col 1)&'((da col 2)/'(da col 1))
draw lda lt none pt circle ptsize .01
lam =(log on am col 1)&' ((am col 2)/'(am col 1))
draw lam
nk1=k1; ns10=s10; k1=ok1; s10=os10
am = points(a,fl)
k1=nk1; s10=ns10
lam =(log on am col 1)&' ((am col 2)/'(am col 1))
draw lam lt dashed
top title "Log-Percent Saturation Plot"
bottom title "log(TOTAL LIGAND)"
left title "(spec. bound)/(total)"
title "[dashed=regression-fit line]" at (.5,.8) fract size .15 inches
title "[solid=MLAB model-fit line]" at (.5,.75) fract size .15 inches
VIEW;
/*Now draw the Scatchard form of the data +fit-curves -------*/
w = ws; unblank w
draw points(lin,0:s10!4) color yellow
TOP TITLE "Scatchard Plot: Bound/Free vs. Bound" color green;
title "[solid=MLAB model-fit line]" at (.5,.8) fract size .14 inches
left title "(bound)/(free)"
bottom title "bound ligand"
lowy=minv(sd col 2); hiy=maxv(sd col 2)
window 0 to 2*s10, lowy to hiy adjust wnice
VIEW;
The MLAB log-file result of running the above do-file on some actual experimental data is shown below.
MLAB Mathematical Modeling System, Revision: April 24, 1996
Copyright: Civilized Software, Inc. (301)962-3711, email: csi@civilized.com
Sat May 18 15:29:38 1996
'* ' is the command prompt
* do liganal
Specify the COLD ligand molecular weight
wc= 1100
Specify the HOT ligand molecular weight
wh= 1130
Specify the half-life in days of the HOT ligand label
hl= 2
Specify the age in days of the HOT ligand label
al= 0
Specify the counting-efficiency (cpm/dpm) of the label
ce= .5
Specify the counting time-period in minutes
ct= 5
Specify the background radioactivity in cpp(counts per period)
br= 0
Specify the specific activity of the HOT ligand(in dpm/mole)
sa= 2.5086e18
Specify the total counts per period of HOT ligand(in cpp)
tc= 65789
Specify the HOT ligand bindability fraction
bd= 1
Specify the Volume (in milliliters)
v= .5
Specify the mass in ng of the HOT ligand
(or enter -1 to have the mass computed for you.)
mh= -1
specified mh value (in ng):
-1
computed mh (hot mass) value (in ng) based on tc:
1.18538739E-2
Specify the number of experimental observation points
nb= 10
type-in the sequence of 10 data points
as: ([COLD ligand mass in ng], [observed bound cpp]) pairs
on successive lines
Type in numbers for KREAD. End lines with ENTER
0 8118
.05 7694
.1 7480
.2 7080
.5 6360
1 6170
3 5397
10 5096
30 5096
1000 4714
Molar conc. of HOT ligand based on supplied molecular wt.
2.09803077E-11
Molar conc. of HOT ligand based on total cpp supplied
2.09803077E-11
D=input data [Cold Ligand (ng) | Hot counts]
D: a 10 by 2 matrix
1: 0 8118
2: 0.05 7694
3: 0.1 7480
4: 0.2 7080
5: 0.5 6360
6: 1 6170
7: 3 5397
8: 10 5096
9: 30 5096
10: 1000 4714
DM=[Cold Ligand (M) | Hot Spec.+Non-Spec.bound(M)]
DM: a 10 by 2 matrix
1: 0 2.58885434E-12
2: 9.09090909E-11 2.45363948E-12
3: 1.81818182E-10 2.38539424E-12
4: 3.63636364E-10 2.25783305E-12
5: 9.09090909E-10 2.02822291E-12
6: 1.81818182E-9 1.96763135E-12
7: 5.45454545E-9 1.72111935E-12
8: 1.81818182E-8 1.62512955E-12
9: 5.45454545E-8 1.62512955E-12
10: 1.81818182E-6 1.50330862E-12
directly-estimated non-spec. binding coef.
C = 7.71837904E-2
MMT=[L Total | B Total | Y Total | F Total]
MMT: a 10 by 4 matrix
1: 2.09803077E-11 1.16933226E-12 1.41952208E-12 1.83914534E-11
2: 1.11889399E-10 5.45935993E-12 7.62606519E-12 9.88039735E-11
3: 2.0279849E-10 9.18445554E-12 1.38730875E-11 1.79740946E-10
4: 3.84616671E-10 1.48997633E-11 2.64914424E-11 3.43225466E-10
5: 9.30071217E-10 2.50658571E-11 6.48466349E-11 8.40158725E-10
6: 1.83916213E-9 4.38447819E-11 1.28640441E-10 1.6666769E-9
7: 5.47552576E-9 6.12326499E-11 3.87952055E-10 5.02634106E-9
8: 1.82027985E-8 1.13851314E-10 1.29613305E-9 1.67928141E-8
9: 5.45664349E-8 3.41291496E-10 3.88541133E-9 5.0339732E-8
10: 1.8182028E-6 1.16933226E-12 1.30280259E-7 1.68792254E-6
MMH=[L Hot | B Hot | Y Hot | F Hot]
MMH: a 10 by 4 matrix
1: 2.09803077E-11 1.16933226E-12 1.41952208E-12 1.83914534E-11
2: 5.96713722E-10 2.91151354E-11 4.06703209E-11 5.26928266E-10
3: 1.9602776E-9 8.87781883E-11 1.34099139E-10 1.73740028E-9
4: 7.05089676E-9 2.73146488E-10 4.85648281E-10 6.29210199E-9
5: 4.12306854E-8 1.11118638E-9 2.87469514E-9 3.72448039E-8
6: 1.61223437E-7 3.84349283E-9 1.12767949E-8 1.46103149E-7
7: 1.42902491E-6 1.59807452E-8 1.012493E-7 1.31179486E-6
8: 1.57929939E-5 9.87789387E-8 1.12454254E-6 1.45696724E-5
9: 1.41918596E-4 8.87644758E-7 1.01053353E-5 1.30925616E-4
10: 0.15756973 1.01337083E-7 1.12903936E-2 .146279336
MMC=[L Cold | B Cold | Y Cold | F Cold]
MMT: a 10 by 4 matrix
1: 2.09803077E-11 1.16933226E-12 1.41952208E-12 1.83914534E-11
2: 1.11889399E-10 5.45935993E-12 7.62606519E-12 9.88039735E-11
3: 2.0279849E-10 9.18445554E-12 1.38730875E-11 1.79740946E-10
4: 3.84616671E-10 1.48997633E-11 2.64914424E-11 3.43225466E-10
5: 9.30071217E-10 2.50658571E-11 6.48466349E-11 8.40158725E-10
6: 1.83916213E-9 4.38447819E-11 1.28640441E-10 1.6666769E-9
7: 5.47552576E-9 6.12326499E-11 3.87952055E-10 5.02634106E-9
8: 1.82027985E-8 1.13851314E-10 1.29613305E-9 1.67928141E-8
9: 5.45664349E-8 3.41291496E-10 3.88541133E-9 5.0339732E-8
10: 1.8182028E-6 1.16933226E-12 1.30280259E-7 1.68792254E-6
Scatchard model linear-regession fit estimates
K1 = 138222119
S10 = 3.0576542E-10
Scatchard model euclidean-fit estimates;
K1 = 287268836
S10 = 1.82633621E-10
final parameter values
value error dependency parameter
1187347821 228157865.8 0.9547016996 K1
4.947046514e-11 8.636211996e-12 0.9633732247 S10
0.0804516126 0.001324755233 0.5724726409 C
19 iterations
CONVERGED
best weighted sum of squares = 4.378871e-11
weighted root mean square error = 2.501106e-06
weighted deviation fraction = 1.716122e-02
R squared = 9.982448e-01
no active constraints
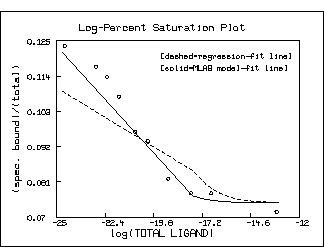
Note that the log-percent saturation plot using the estimated values for K1 and S10 obtained by linear-regression with the bound/free vs. bound Scatchard-plot form of the data is decidedly inferior to the graph using the direct saturation model-based estimates. Of course, as the following picture shows, this situation is not so clear in the Scatchard plot itself. But the log-percent saturation plot is the more faithful form of the data with regard to minimal error in the -values, and thus the associated estimated parameters are likely to be the most accurate.
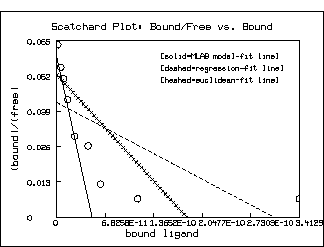
You can see that MLAB is an extremely flexible and general tool for curve-fitting. Moreover, it has a broad range of other useful functions, only a few of which have been alluded to here.